Filsafat Matematika

Filsafat Matematika  

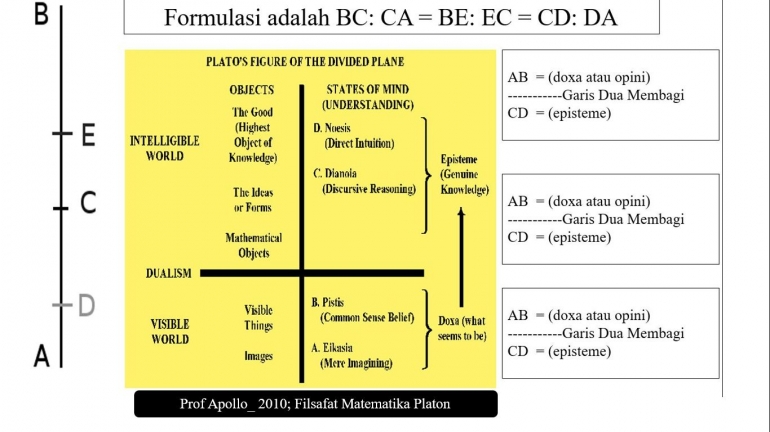
Tulisan ini saya kutib dari teks Matematika dan Dialektika  pada teks buku the Republic  Platon buku VI-VII.    Platon menulis The Republic sekitar 375 SM, sebelum Euclid menulis The Elements. Dalam karya ini, Platon mengemukakan gagasannya tentang pendidikan. 

Untuk ini, Platon percaya, seseorang harus mempelajari lima disiplin matematika, yaitu aritmatika, geometri bidang, geometri padat, astronomi, dan harmonik. Setelah menguasai matematika, maka seseorang dapat melanjutkan ke studi filsafat. 

Pertama Platon memberikan gambaran tentang ide-ide pendidikannya, kemudian melanjutkan pembicaraan tentang lima disiplin matematika. Sebelum kita memberikan versi deskripsi Platon seperti yang diberikan di The Republic, mari diperhatikan gaya penulisannya. Platon, sebagai narator, menggambarkan percakapan yang dilakukan dengan kakaknya Glaucon, yang menyebut narator sebagai Socrates.

Platon berpendapat manfaat belajar berhitung;

"Dan di kelas manakah persatuan dan angka itu milik?"

"Aku tidak tahu," jawabnya.

'Pikirkan sedikit,' kataku kepadanya, 'dan kamu akan melihat  apa yang telah terjadi sebelumnya akan memberikan jawaban; karena jika persatuan sederhana dapat dirasakan secara memadai oleh penglihatan atau oleh indera lain, maka, tidak akan ada yang menarik pikiran menuju kenyataan lebih daripada dalam kasus jari yang kita diskusikan. 

Tetapi ketika dikombinasikan dengan persepsi yang berlawanan, dan tampaknya melibatkan konsepsi pluralitas sebanyak kesatuan, maka pikiran mulai timbul dalam diri kita, dan jiwa bingung dan ingin sampai pada suatu keputusan bertanya "Apa yang mutlak kesatuan?" Ini adalah cara di mana studi tentang seseorang memiliki kekuatan menggambar dan mengubah pikiran menjadi kontemplasi realitas.  

'Dan tentu saja,' katanya, 'karakteristik ini terjadi dalam kasus satu; karena kita melihat hal yang sama menjadi satu dan tak terbatas dalam jumlah banyak? '

"Ya," kataku, "dan ini benar, harus sama benarnya dengan semua angka?"

'Pasti.'

"Dan semua perhitungan dan perhitungan berkaitan dengan angka?"

'Iya.'

"Dan mereka berdua tampaknya menuntun pikiran menuju kebenaran?"

"Ya, dengan cara yang sangat luar biasa."

'Maka ini adalah pengetahuan tentang jenis yang kita cari, memiliki penggunaan ganda, militer dan filosofis; karena prajurit harus mempelajari seni angka atau dia tidak akan tahu bagaimana mengatur pasukannya, dan juga filsuf, karena dia harus bangkit dari dunia sementara dan memahami realitas, dan oleh karena itu dia harus dapat menghitung. '

'Itu benar.'

"Dan wali kita adalah prajurit dan filsuf?"

'Pasti.'

'Maka ini adalah semacam pengetahuan yang harus dijadikan subjek studi oleh undang-undang; dan kita harus berusaha untuk membujuk mereka yang berada dalam posisi otoritas di Negara kita untuk pergi dan belajar aritmatika, bukan sebagai amatir, tetapi mereka harus melanjutkan penelitian sampai mereka benar memahami sifat angka; tidak juga, seperti pedagang atau pedagang eceran, dengan maksud untuk membeli atau menjual, tetapi demi penggunaan militer mereka, dan pikiran itu sendiri; dan karena ini akan menjadi cara termudah untuk lulus dari dunia menjadi dunia kebenaran dan realitas. '

"Itu luar biasa," katanya.

'Ya,' kataku, 'dan sekarang setelah membicarakannya, aku harus menambahkan betapa menawannya ilmu hitung! dan dalam berapa banyak cara itu adalah alat yang halus dan berguna untuk mencapai tujuan kita, jika dikejar dalam semangat filsuf, dan bukan penjaga toko! '

'Bagaimana maksudmu?', Dia bertanya.

sumber: dokpri

Maksud saya, seperti yang saya katakan,  aritmatika memiliki efek yang sangat besar dan tinggi, memaksa pikiran untuk berpikir tentang angka abstrak, dan memberontak terhadap pengenalan benda-benda yang terlihat atau berwujud ke dalam argumen. 

Anda tahu betapa mantapnya para ahli seni menentang dan mengolok-olok siapa pun yang mencoba untuk membagi kesatuan absolut ketika dia menghitung, dan jika Anda membaginya, mereka melipatgandakannya, berhati-hati agar seseorang tidak pernah terbukti mengandung banyak bagian. . '

'Itu benar sekali.'

'Sekarang, seandainya seseorang berkata kepada mereka, Glaucon, "Wahai teman-teman, apa angka-angka yang indah tentang yang Anda alasankan, di mana, seperti yang Anda katakan, ada unit konstituen, seperti yang Anda minta, dan setiap unit sama dengan satu sama lain, tidak berubah-ubah, dan tidak dapat dibagi menjadi beberapa bagian, "- apa yang akan mereka jawab? '

"Mereka akan menjawab, seperti yang seharusnya saya pikirkan,  mereka berbicara tentang angka-angka yang hanya dapat direalisasikan dalam pikiran, dan tidak ada cara lain untuk menangani mereka."

'Kalau begitu, Anda tahu,' saya tunjukkan kepadanya, ' pengetahuan ini mungkin benar-benar disebut perlu, membutuhkan pikiran, seperti yang jelas-jelas terjadi, untuk menggunakan kecerdasan murni dalam mencapai kebenaran murni?'

'Iya; itulah efeknya, 'dia setuju.

'Dan inilah poin lain,  mereka yang memiliki bakat alami untuk perhitungan pada umumnya cepat pada setiap jenis pengetahuan lainnya; dan bahkan orang yang lamban jika mereka memiliki pelatihan aritmatika, meskipun mereka tidak mendapatkan manfaat lain darinya, selalu menjadi jauh lebih cepat daripada yang seharusnya. '

"Sangat benar," katanya.

'Dan memang, kamu tidak akan dengan mudah menemukan pelajaran yang lebih sulit, yang semakin sulit bagi mereka yang belajar dan mempraktikkannya.'

'Anda tidak akan.'

"Dan, untuk semua alasan ini, aritmatika adalah sejenis pengetahuan di mana warga yang paling cerdas harus dilatih, dan yang tidak boleh dilepaskan."

'Saya setuju.'

Platon berpendapat manfaat geometri bidang pembelajaran Argumen Platon di sini pada dasarnya serupa dengan yang digunakan untuk menganjurkan studi aritmatika. Itu tidak harus dipelajari untuk kegunaan praktisnya tetapi untuk melatih pikiran.

'Biarlah aritmatika menjadi yang pertama dari mata pelajaran kita. Dan selanjutnya, akankah kita bertanya apakah sains sejenis juga menyangkut kita? '

"Maksudmu geometri ?," dia bertanya.

"Tepat sekali."

'Jelas,' katanya, 'kami memperhatikan bagian geometri yang berhubungan dengan perang; karena dalam mendirikan kemah, atau mengambil posisi, atau menutup atau memperluas garis pasukan, atau manuver militer lainnya, baik dalam pertempuran sebenarnya atau dalam pawai, itu akan membuat perbedaan apakah jenderal tidak atau tidak kenal geometri. '

'Ya,' kataku, 'tetapi untuk tujuan itu sedikit geometri atau aritmatika akan cukup; pertanyaannya lebih berkaitan dengan bagian geometri yang lebih besar dan lebih maju - apakah itu cenderung dalam tingkat apa pun untuk membuat lebih mudah visi gagasan baik; dan , seperti yang saya katakan, semua hal cenderung memaksa pikiran untuk mengalihkan perhatiannya ke tempat itu, di mana kesempurnaan sepenuhnya berada, yang harus dilihat, dengan segala cara, untuk dilihat. '

"Benar," katanya.

'Kemudian jika geometri memaksa kita untuk melihat kenyataan, itu menyangkut kita; jika ranah perubahan saja, itu bukan urusan kita? '

"Ya, itulah yang kami klaim."

"Namun siapa pun yang memiliki paling sedikit kenalan dengan geometri tidak akan menyangkal  konsepsi sains semacam itu sangat bertentangan dengan istilah-istilah biasa dari mereka yang menggunakannya."

'Bagaimana?'

'Mereka dalam praktiknya hanya dalam pandangan, dan selalu berbicara dengan cara yang sempit dan konyol, tentang "mengkuadratkan" dan "memperluas" dan "menerapkan" dan sejenisnya - mereka membingungkan cara geometri dengan cara-cara kehidupan sehari-hari; sedangkan pengetahuan adalah objek nyata dari keseluruhan sains. '

"Tentu saja itu sangat benar," katanya.

"Kalau begitu, haruskah kita membuat penerimaan lebih lanjut?"

"Pengakuan apa?"

 pengetahuan yang menjadi tujuan geometri adalah pengetahuan tentang yang abadi, dan bukan tentang sesuatu yang sementara yang akan membusuk. '

'Itu,' jawabnya, 'dapat dengan mudah diizinkan, dan memang benar  pengetahuan geometri itu abadi.'

"Kalau begitu, sahabatku yang terhormat, geometri akan menarik pikiran ke arah kebenaran, dan menciptakan semangat filsafat, dan membangkitkan apa yang sekarang dengan sedihnya dibiarkan jatuh."

"Tidak ada yang lebih mungkin memiliki efek seperti itu."

'Maka tidak ada yang harus lebih kuat dari yang dibutuhkan oleh penghuni Negara Anda untuk belajar geometri. Selain itu, sains juga memiliki kelebihan tidak langsung, yang tidak sedikit. '

"Dari jenis apa?" dia berkata.

"Ada kelebihan militer yang kamu bicarakan," kataku, "dan di semua departemen pengetahuan, seperti yang dibuktikan oleh pengalaman, siapa pun yang telah mempelajari geometri jauh lebih cepat dalam mempelajari mata pelajaran lain daripada yang tidak."

"Ya, memang," katanya, "ada perbedaan tak terbatas di antara mereka."

'Kalau begitu, akankah kita mengusulkan ini sebagai cabang ilmu pengetahuan kedua yang harus dipelajari oleh remaja kita?'

"Mari kita lakukan," jawabnya.

Platon berpendapat manfaat mendukung geometri padat: ["Jelaslah  geometri yang solid relatif tidak berkembang ketika Platon menulis The Republic sehingga ia berpendapat kuat  studinya harus didorong"]

"Dan seandainya kita menjadikan astronomi subjek ketiga - apa yang Anda katakan?"

"Saya sangat tertarik pada hal itu," katanya, "pengamatan musim dan bulan dan tahun adalah sangat penting bagi jenderal seperti halnya bagi petani atau pelaut."

"Aku merasa geli," kataku, "pada ketakutanmu akan ketidaksetujuan publik, yang membuatmu berjaga-jaga terhadap kesan menuntut studi yang tampaknya tidak berguna; dan saya cukup mengakui kesulitan mempercayai  di dalam setiap orang ada kemampuan pikiran yang, ketika telah dibutakan dan dihancurkan oleh pengejaran lain, adalah dengan ini dimurnikan dan diterangi ulang; dan bernilai jauh lebih dari sepuluh ribu mata, karena hanya dengan itu kebenaran terlihat. 

Sekarang ada dua tipe orang: satu tipe yang akan setuju dengan Anda dan akan menerima proposal Anda dengan persetujuan tanpa pengecualian; tipe lain kepada siapa mereka akan sepenuhnya omong kosong, dan yang secara alami akan menganggap mereka sebagai dongeng, karena mereka tidak melihat keuntungan apa pun yang dapat diperoleh dari mereka. 

Dan karena itu Anda sebaiknya memutuskan sekaligus dengan mana dari dua jenis yang Anda usulkan untuk berdebat. Anda kemungkinan besar tidak akan berkata apa-apa, dan  tujuan utama Anda dalam mengajukan argumen adalah untuk kemajuan Anda sendiri; pada saat yang sama Anda tidak mendendam orang lain atas manfaat yang mungkin mereka terima.

"Kurasa," jawabnya, " aku lebih suka melanjutkan argumen terutama untuk kepuasanku sendiri."

"Kalau begitu, mundurlah, karena kita salah dalam urutan ilmu pengetahuan setelah geometri bidang."

"Apa kesalahannya?" dia berkata.

"Setelah geometri bidang," kataku, "kami langsung menuju padatan dalam revolusi, bukannya mengambil padatan dalam diri mereka sendiri; sedangkan setelah dimensi kedua, yang ketiga, yang berkaitan dengan kubus dan dimensi kedalaman, seharusnya mengikuti. '

"Itu benar, Socrates, tetapi sedikit sekali yang diketahui tentang masalah ini."

'Wah, ya,' kataku, 'dan karena dua alasan: - pertama-tama, tidak ada pemerintah yang menghargai hal itu; ini mengarah pada kurangnya energi dalam mengejar itu, dan itu sulit. Di tempat kedua, siswa tidak dapat mempelajarinya kecuali mereka memiliki guru. 

Tetapi kemudian seorang guru hampir tidak dapat ditemukan, dan bahkan jika dia bisa, seperti yang sekarang terjadi, para siswa, yang sangat sombong, tidak akan mendengarkannya. 

Namun, itu akan menjadi sebaliknya jika seluruh Negara menjadi direktur studi ini dan memberi nilai pada mereka; kemudian para murid ingin maju, dan akan ada investigasi yang berkelanjutan dan sungguh-sungguh, dan penemuan akan dibuat; karena bahkan sekarang, tidak dipedulikan oleh dunia, dan diberi perlakuan yang tidak memadai, dan meskipun masyarakat maupun siswa tidak memahami kegunaan nyata mereka, masih saja studi-studi ini membuat kemajuan dengan daya tarik alami mereka, dan sangat mungkin, jika mereka mendapat bantuan dari Negara. , suatu hari mereka akan muncul menjadi terang. '

"Ya," katanya, "ada daya tarik besar di dalamnya. Tapi saya tidak mengerti dengan jelas perubahan urutannya. Pertama Anda mulai dengan geometri permukaan bidang? '

"Ya," kataku.

"Kamu pertama-tama menempatkan astronomi, dan kemudian kamu kembali pada apa yang kamu katakan?"

"Ya, semakin tergesa-gesa semakin sedikit kecepatan," kataku. "Dengan tergesa-gesa, keadaan geometri padat yang menggelikan, yang, menurut aturan alami, seharusnya mengikuti, membuatku melewati cabang ini dan melanjutkan ke astronomi, atau gerakan benda padat."

"Benar," katanya.

'Kalau begitu dengan anggapan  sains yang sekarang dihilangkan akan muncul jika didorong oleh Negara, mari kita lanjutkan ke astronomi, yang akan menjadi subjek keempat.'

Platon berpendapat manfaat astronomi;

 Kami mencatat di sini  Platon memiliki tujuan untuk melatih pikiran. Dia menciptakan silabus yang memungkinkan siswa untuk melakukan sesuatu untuk diri mereka sendiri. Dia tidak menganjurkan studi ilmu-ilmu fisika dalam hak mereka sendiri dalam konteks ini, demikian juga terhadap pengamatan astronomi. Dia, bagaimanapun, sangat berpendapat  astronom membutuhkan alat matematika

"Perintah yang tepat," jawabnya. 'Dan sekarang, Socrates, ketika Anda menegur cara vulgar di mana saya memuji astronomi sebelumnya, pujian saya sekarang akan diberikan dalam semangat Anda sendiri. Untuk semua orang, saya pikir, harus melihat  astronomi memaksa pikiran untuk melihat ke atas dan menuntun kita dari bumi ke surga. '

"Setiap orang kecuali aku sendiri," kataku, "untuk semua orang ini mungkin jelas, tetapi itu bukan untukku."

"Lalu apa yang akan Anda katakan?"

"Aku lebih baik mengatakan  mereka yang mengangkat astronomi menjadi filsafat bagiku membuat kita melihat ke bawah dan bukan ke atas."

'Maksud kamu apa?' Dia bertanya.

'Kamu,' jawab saya, 'ada dalam benakmu konsepsi yang benar-benar luhur tentang pengetahuan kita tentang hal-hal di atas. Dan saya berani mengatakan  jika seseorang harus menengadahkan kepalanya dan mempelajari langit-langit yang dicat, Anda masih akan berpikir  pikirannya sedang digunakan, dan bukan matanya. 

Dan Anda sangat mungkin benar, dan saya mungkin bodoh: tetapi, menurut saya, hanya pengetahuan yang nyata dan tidak terlihat yang dapat membuat pikiran melihat ke atas. 

Dan apakah seseorang menganga di langit atau mengedipkan mata di tanah, mencari untuk mempelajari suatu perasaan tertentu, saya akan menyangkal  dia dapat belajar, karena tidak ada yang semacam itu adalah pengetahuan sains; pikirannya melihat ke bawah, bukan ke atas, apakah jalannya menuju pengetahuan adalah dengan air atau darat, apakah ia mengapung, atau hanya berbaring di punggungnya. '

"Aku menerima," katanya,  aku harus dimarahi. Namun, saya ingin memastikan bagaimana astronomi harus dipelajari dengan cara apa pun yang lebih berkaitan dengan pengetahuan yang sedang kita bicarakan? '

"Aku akan memberitahumu," kataku. 'Langit berbintang yang kita lihat adalah yang terbaik dan paling sempurna dari benda-benda yang terlihat, tetapi itu pasti harus dianggap jauh lebih rendah, hanya karena mereka terlihat, dengan gerakan sejati kecepatan cepat dan kelambatan mutlak, yang relatif terhadap masing-masing lain. 

Realitas kecepatan sebenarnya ditemukan dalam jumlah murni dan dalam setiap figur sempurna. Sekarang, ini harus dipahami dengan alasan dan kecerdasan, tetapi tidak dengan penglihatan. Apa kamu setuju?'

"Ya," jawabnya.

'Well, kalau begitu,' aku melanjutkan, 'kemegahan langit yang terlihat harus digunakan sebagai ilustrasi dengan maksud untuk pengetahuan yang lebih tinggi itu; kecantikan mereka seperti keindahan figur atau gambar yang digambar dengan sangat baik oleh tangan Daedalus, atau artis atau juru gambar hebat lainnya, yang mungkin kita saksikan. 

Siapa pun yang memahami geometri yang melihat mereka akan menghargai kehebatan pengerjaan mereka, tetapi ia tidak akan pernah bermimpi berpikir  di dalam mereka ia dapat mempelajari kebenaran tentang kesetaraan atau tentang penggandaan, atau kebenaran tentang proporsi lainnya. '

'Tidak,' jawabnya, 'gagasan seperti itu akan masuk akal.'

"Dan bukankah astronom sejati akan memiliki perasaan yang sama ketika dia melihat pergerakan bintang-bintang?" Saya bertanya. 'Apakah dia tidak akan berpikir  langit dan benda-benda langit disatukan oleh Pencipta mereka dengan cara yang paling sempurna? 

Tetapi ia tidak akan pernah membayangkan  proporsi malam dan siang, atau keduanya terhadap bulan, atau dari bulan ke tahun, atau periode bintang-bintang untuk ini dan satu sama lain, dan hal-hal lain yang material dan terlihat bisa juga kekal dan tidak mengalami penyimpangan - itu tidak masuk akal; dan sama tidak masuk akal untuk bersusah payah menyelidiki kebenaran mereka yang sebenarnya. '

"Aku setuju," jawabnya, "meskipun aku tidak pernah memikirkan ini sebelumnya."

'Kalau begitu,' kataku, 'dalam astronomi, seperti dalam geometri, kita harus mengatur masalah yang harus dipecahkan, dan meninggalkan surga yang terlihat sendiri jika kita ingin mendekati subjek dengan cara yang benar dan dengan demikian menempatkan karunia alami alasan untuk tujuan nyata. '

"Itu," katanya, "adalah karya yang jauh melebihi para astronom kita saat ini."

'Ya,' kataku, 'dan ada banyak hal lain yang juga harus diberikan perpanjangan yang serupa kepada mereka, jika undang-undang kita memiliki nilai apa pun. Tetapi bisakah Anda memberi tahu saya tentang studi lain yang cocok? '

"Tidak," katanya, "bukan tanpa memikirkannya."

Platon mengemukakan manfaat harmonic: Di sini Platon memberikan argumen yang mirip dengan yang digunakan ketika ia membahas astronomi.

'Gerak,' kataku, 'memiliki banyak bentuk, dan bukan hanya satu. Dua dari mereka cukup jelas bahkan untuk otak tidak lebih baik dari kita; tetapi ada yang lain, seperti yang saya bayangkan, yang mungkin diserahkan kepada para ahli. '

"Tapi apa keduanya?"

"Ada yang kedua," kataku, "yang merupakan pasangan dari yang sudah disebutkan."

'Dan apa itu?'

"Yang kedua," kataku, "tampaknya berhubungan dengan telinga dengan cara yang sama dengan yang pertama berhubungan dengan mata. Karena saya percaya  ketika mata dirancang untuk memandang bintang-bintang, maka apakah telinga dirancang untuk mendengar gerakan harmoni, dan ini adalah ilmu pengetahuan saudara - seperti yang dikatakan oleh para pengikut Pythagoras, dan kita, Glaucon, setuju dengan mereka? '

"Ya," jawabnya.

'Tapi ini,' kataku, 'adalah studi yang panjang dan sulit, dan oleh karena itu kita sebaiknya pergi dan berkonsultasi dengan mereka tentang masalah ini dan mereka akan memberi tahu kita apakah ada aplikasi lain dari ilmu-ilmu ini. Pada saat yang sama, kita tidak boleh melupakan prinsip kita yang lebih tinggi. '

'Apa itu?'

'Ada tingkat yang harus dicapai semua pengetahuan, dan yang harus dicapai oleh murid kita, dan jangan sampai gagal, seperti yang saya katakan  mereka lakukan dalam astronomi. Karena dalam ilmu harmoni, seperti yang mungkin Anda ketahui, hal yang sama terjadi. Para guru harmoni membandingkan suara dan konsonan yang dapat didengar, dan kerja keras mereka, seperti halnya para astronom, sia-sia. '

"Ya, di surga!" dia berkata, 'dan itu sama bagusnya dengan permainan untuk mendengar mereka berbicara tentang catatan mereka yang kental, sebagaimana mereka menyebutnya. 

Mereka mendekatkan telinganya di samping senar seperti orang yang mencoba mendengar suara melalui dinding tetangga mereka - beberapa dari mereka menyatakan  mereka dapat membedakan not menengah dan telah menemukan interval terkecil yang seharusnya menjadi satuan pengukuran, sementara yang lain bersikeras  tidak ada perbedaan antara kedua not - keduanya banyak menempatkan telinga mereka sebelum pemahaman mereka. '

"Maksudmu," kataku, "tuan-tuan yang menggoda dan menyiksa senar dan memuntirnya pada pasak instrumen. Saya mungkin melanjutkan metafora dan berbicara dengan cara mereka tentang pukulan yang diberikan plectrum, dan membuat tuduhan terhadap string, baik keterbelakangan dan kedepan untuk terdengar - tetapi ini akan membosankan, dan karena itu saya hanya akan mengatakan  ini bukan laki-laki, dan yang saya maksud adalah Pythagoras, yang baru saja saya usulkan untuk menanyakan tentang harmoni. 

Karena mereka juga salah dengan cara yang sama seperti para astronom. Mereka menyelidiki hubungan numerik antara harmoni yang didengar, tetapi mereka tidak pernah mendapatkan sejauh merumuskan masalah - yaitu, mereka tidak pernah mencapai harmoni alami angka, atau mencerminkan mengapa beberapa angka harmonis dan yang lainnya tidak. '

"Itu," katanya, "akan menjadi pekerjaan yang menakutkan."

'Namun demikian, satu hal,' jawab saya, 'yang saya sebut berguna, yaitu, jika diselidiki dengan maksud untuk yang indah dan baik. Tetapi jika mengejar roh lain, itu tidak berguna. '

"Sangat benar," katanya.