Filsafat Matematika Descartes [3]

Tulisan berikut ini adalah esensi pada gagasan matematika Rene Descartes dalam buku 1, dan buku 2 sebagai dasar matematika ekonomi di program pascarsajana dalam bidang ekonometrika atau singkatan ekonomi, matematika, dan statistika

Buku Dua dari La Geometrie berjudul "On the Nature of Curved Lines" dan dimulai dengan perbedaan terkenal antara kurva "geometrik" dan "mekanis" Descartes. Mengingat pentingnya untuk memahami program La Geometrie serta perhatian perbedaan ini telah diambil dari komentator, ada baiknya memeriksa proposal yang dibuat di halaman pembuka Buku Dua dengan hati-hati.

Descartes dimulai dengan mengacu pada klasifikasi masalah kuno dan menawarkan interpretasinya tentang bagaimana ahli matematika kuno membedakan kurva yang dapat digunakan dalam solusi untuk masalah geometri dari yang tidak bisa:

Orang dahulu akrab dengan fakta masalah geometri dapat dibagi menjadi tiga kelas, yaitu, bidang, masalah solid, dan linier. Ini sama dengan mengatakan beberapa masalah hanya memerlukan lingkaran dan garis lurus untuk konstruksi mereka, sementara yang lain memerlukan bagian kerucut dan yang lain lagi kurva yang lebih kompleks.

Namun, saya terkejut mereka tidak melangkah lebih jauh, dan membedakan antara tingkat yang berbeda dari kurva yang lebih kompleks, saya juga tidak melihat mengapa mereka menyebut yang disebut terakhir dengan mekanik, daripada geometris. Jika mengatakan itu disebut mekanis karena semacam instrumen harus digunakan untuk menggambarkannya, maka harus, agar konsisten, menolak lingkaran dan garis lurus, karena ini tidak dapat dijelaskan di atas kertas tanpa menggunakan kompas dan penggaris. , yang juga dapat disebut instrumen.

Itu bukan karena instrumen lain, yang lebih rumit daripada penggaris dan kompas, karena itu kurang akurat, karena jika demikian mereka harus dikeluarkan dari mekanika, di mana akurasi konstruksi bahkan lebih penting daripada dalam geometri. Dalam yang terakhir, ketepatan nalar saja dicari, dan ini pasti bisa menyeluruh dengan mengacu pada garis-garis seperti yang lebih sederhana (G, 40-44).

Descartes menyiratkan istilah "mekanis" dan "non-geometris" adalah identik dalam matematika kuno, meskipun sama sekali tidak jelas ini adalah makna yang dimaksudkan dari istilah "mekanis." Yaitu, tidak jelas, mengingat bukti tekstual yang tersedia, klasifikasi kurva menjadi "geometris" dan "mekanik" dimaksudkan untuk berfungsi sebagai klaim normatif mengenai legitimasi penggunaan kurva dalam pemecahan masalah geometris.

Ini bisa dengan mudah dibaca sebagai moniker deskriptif yang menangkap berbagai cara di mana kurva dibangun campuran Descartes tentang deskriptif dan normatif dalam proposal 1619 untuk proposal " ilmu baru "geometri).

Di samping Descartes membaca tentang nenek moyang, yang penting untuk memahami interpretasinya sendiri yang unik tentang kurva geometris adalah perbedaan yang ia tarik antara "akurasi konstruksi" dari sebuah kurva, yang ia berikan masalah untuk mekanik, dan "ketepatan penalaran," "Yang ia anggap sebagai satu-satunya persyaratan untuk menerima kurva sebagai geometri yang sah.

Dalam membuat klaim ini, Descartes sedang mengukir tempat yang unik untuk gagasannya tentang kurva geometris: Dia meninggalkan kriteria "ketepatan konstruksi" yang diadopsi Clavius dalam karya-karya awalnya untuk membuat kurva yang dapat diterima dalam pemecahan masalah geometri dan juga klaim yang diteruskan oleh Viete kurva yang dibangun secara instrumen tidak dianggap geometris.

Seperti yang disiratkan oleh presentasi Descartes, kedua kriteria ini membingungkan masalah mekanika dengan "ketepatan penalaran" yang merupakan satu-satunya perhatian geometri. Dengan demikian, ketika Buku Dua berlanjut, Descartes menegaskan kembali untuk menentukan status geometrik kurva harus meletakkan fokus pada masalah-masalah penalaran yang tepat dan jelas dan, khususnya, pada pertanyaan apakah kurva dapat dibangun dengan gerakan yang tepat dan jelas. Setelah mempresentasikan postulat "dua atau lebih garis dapat digerakkan, satu demi satu, menentukan dengan persimpangan mereka kurva lainnya," Descartes menjelaskan,

Memang benar bagian kerucut tidak pernah bebas diterima ke dalam geometri kuno, dan saya tidak peduli untuk melakukan perubahan nama yang dikonfirmasi oleh penggunaan; namun demikian, tampak sangat jelas bagi saya jika membuat asumsi biasa geometri itu tepat dan tepat, sedangkan mekanika tidak; dan jika menganggap geometri sebagai ilmu yang memberikan pengetahuan umum tentang pengukuran semua benda, maka tidak punya hak lagi untuk mengecualikan kurva yang lebih kompleks daripada kurva yang lebih sederhana, asalkan itu dapat dipahami seperti dijelaskan oleh gerak terus menerus atau dengan beberapa gerakan berturut-turut, setiap gerakan sepenuhnya ditentukan oleh gerakan sebelumnya; karena dengan cara ini pengetahuan yang tepat tentang besarnya masing-masing selalu diperoleh (G, 43).

Melihat dalam pernyataan ini ketepatan dan ketepatan geometri terkait erat dengan pertimbangan geometer tentang gerakan yang dapat dilacak secara tepat dan tepat. Yaitu, geometer dibenarkan dalam menggunakan kurva sederhana serta kurva yang lebih kompleks, selama konstruksi kurva ini berlangsung dengan gerakan "tepat dan tepat".

Descartes mengklarifikasi bagaimana sebuah kurva kompleks "dapat dipahami seperti yang dijelaskan oleh gerakan terus menerus atau dengan beberapa gerakan berturut-turut, setiap gerakan sepenuhnya ditentukan oleh mereka yang mendahului" dengan menghadirkan kompas mesolabe yang pertama kali dikembangkannya pada tahun 1619:

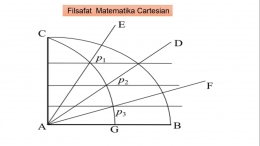
Pertimbangkan garis AB, AD, AF, dan sebagainya, yang anggap dapat digambarkan dengan menggunakan instrumen YZ [Gambar 3]. Instrumen ini terdiri dari beberapa penggaris yang disatukan sedemikian rupa sehingga YZ ditempatkan di sepanjang garis AN sudut XYZ dapat ditingkatkan atau dikurangi ukurannya, dan ketika sisinya disatukan, titik B, C, D, E, F, G, H, semua bertepatan dengan A; tetapi ketika ukuran sudut bertambah, penguasa BC, diikat pada sudut kanan ke XY di titik B, mendorong ke arah Z penguasa CD yang meluncur sepanjang YZ selalu di sudut kanan.

Dengan cara yang sama, CD mendorong DE yang meluncur sepanjang YX selalu sejajar dengan BC; DE mendorong EF; EF mendorong FG; FG mendorong GH, dan sebagainya. Dengan demikian dapat membayangkan tak terbatas penguasa, masing-masing mendorong yang lain, setengah dari mereka membuat sudut yang sama dengan YX dan sisanya dengan YZ.

Sekarang ketika sudut XYZ dinaikkan, titik B menggambarkan kurva AB, yang merupakan lingkaran; sedangkan persimpangan dari penguasa lainnya, yaitu, titik D, F, H menggambarkan kurva lainnya, AD, AF, AH, di mana yang terakhir lebih kompleks daripada yang pertama dan ini lebih kompleks daripada lingkaran.

Namun demikian saya tidak melihat alasan mengapa deskripsi dari yang pertama tidak dapat dipahami dengan jelas dan sejelas itu dari lingkaran, atau setidaknya sebagai bagian dari kerucut; atau mengapa yang kedua, ketiga, atau lainnya yang dapat dengan demikian dijelaskan, tidak dapat dengan jelas dipahami sebagai yang pertama: dan karena itu saya tidak melihat alasan mengapa mereka tidak boleh digunakan dengan cara yang sama dalam penyelesaian masalah geometris (G, 44--47).

Beberapa poin patut ditekankan. Pertama, Descartes menyajikan kurva yang lebih kompleks yang dihasilkan oleh kompasnya seperti yang dijelaskan oleh gerakan yang dapat "dipahami dengan jelas dan berbeda" seperti gerakan yang diperlukan untuk membangun lingkaran yang lebih sederhana. Dan karena gerakan jelas dan berbeda yang diperlukan untuk konstruksi mereka, kurva ini secara geometris sah.

Artinya, konsisten dengan kriteria umum Descartes untuk membangun kurva geometris, kurva kompleks ini dapat digunakan dalam solusi masalah geometris. Kedua, melihat meskipun Descartes berhati-hati untuk membedakan keprihatinan geometri dari orang-orang mekanik, ia tidak menjauhi konstruksi kurva dengan menggunakan instrumen.

Meskipun konstruksi instrumental adalah konstruksi mekanis, mereka tetap dapat memunculkan kurva geometris justru karena gerakan instrumen dikandung dengan "jelas dan jelas". gerakan dihasilkan oleh instrumen tidak membuat kurva yang dihasilkan non-geometris. (Untuk lebih lanjut tentang penggunaan instrumen di La Geometrie)

Dalam nada yang sama, kurva yang non-geometris menurut standar Descartes adalah kurva yang membutuhkan gerakan yang lebih rumit, kurang jelas dan berbeda untuk konstruksinya. Dia menjelaskan:

Mungkin penjelasan nyata dari penolakan geometer kuno untuk menerima kurva lebih kompleks daripada bagian kerucut terletak pada kenyataan kurva pertama yang menarik perhatian mereka terjadi adalah spiral, quadratrix, dan kurva serupa, yang benar-benar menjadi milik hanya untuk mekanik, dan bukan di antara kurva yang saya pikir harus dimasukkan di sini, karena mereka harus dipahami seperti yang dijelaskan oleh dua gerakan terpisah yang hubungannya tidak mengakui penentuan yang tepat (G, 44).

Descartes secara eksplisit menyebut spiral dan quadratrix sebagai kurva yang konstruksinya "harus dipahami seperti yang dijelaskan oleh dua gerakan terpisah yang hubungannya tidak mengakui penentuan yang tepat." Kemudian dalam Buku Dua ia menjelaskan mengapa deskripsi seperti itu gagal dipahami dengan jelas dan jelas:

geometri seharusnya tidak termasuk garis yang seperti string, dalam arti kadang-kadang lurus dan kadang-kadang melengkung, karena rasio antara garis lurus dan kurva tidak diketahui, dan saya percaya tidak dapat ditemukan oleh pikiran manusia, dan karena itu tidak ada kesimpulan berdasarkan rasio tersebut dapat diterima sebagai ketat dan tepat (G, 91).

Dengan pernyataan ini, masalah mendasar dari spiral, quadratrix, dan "garis yang seperti string" adalah konstruksi mereka memerlukan pertimbangan rasio, atau hubungan, antara lingkaran dan garis lurus. Pertimbangkan spiral. Seperti yang lihat di atas, konstruksinya melibatkan dua gerakan yang seragam: gerakan bujursangkar yang seragam dari suatu titik di sepanjang segmen dan gerakan melingkar seragam dari segmen di se r titik.

Kedua gerakan ini harus dipertimbangkan secara simultan agar jalur titik bergerak untuk menggambarkan spiral, dan ini, bagi Descartes, adalah yang pada akhirnya bermasalah. Pikiran manusia dapat berpikir tentang gerakan simultan bujursangkar dan melingkar, tetapi tidak dapat melakukannya dengan kejelasan dan perbedaan yang diperlukan untuk memenuhi standar geometri yang tepat dan ketat.

Setelah menyajikan kriteria konstruksinya untuk kurva geometris, Descartes mengembangkan koneksi novelnya antara konstruksi geometris dan representasi aljabar kurva ini. Sedangkan dalam Buku Satu Descartes merinci bagaimana menggunakan aljabar untuk menetapkan solusi masalah geometris ada, di sini, di Buku Dua, Descartes mengusulkan hubungan yang lebih kuat antara aljabar dan geometri dan terkenal mengklaim setiap kurva geometris yang sah dapat diwakili oleh persamaan:

Di sini saya bisa memberikan beberapa cara lain untuk melacak dan membayangkan serangkaian garis lengkung, masing-masing kurva lebih kompleks daripada yang sebelumnya, tetapi saya pikir cara terbaik untuk mengelompokkan semua kurva tersebut dan kemudian mengklasifikasikannya dalam urutan, adalah dengan mengenali fakta semua titik kurva yang dapat sebut "geometris," yaitu, yang mengakui pengukuran yang tepat dan tepat, harus menanggung hubungan yang pasti dengan semua titik dari garis lurus, dan hubungan ini harus dinyatakan dengan sarana dari persamaan tunggal (G, 48).

Dia kemudian mulai mengklasifikasikan kurva "geometris" ini sesuai dengan derajat persamaan yang sesuai, mengklaim:

Jika persamaan [kurva] tidak mengandung istilah dengan tingkat yang lebih tinggi dari [produk] segi empat dua kuantitas yang tidak diketahui, atau kuadrat dari satu, kurva milik kelas pertama dan paling sederhana, yang hanya berisi lingkaran, parabola, hiperbola , dan elips; tetapi ketika persamaan mengandung satu atau lebih istilah dari tingkat ketiga atau keempat, dalam satu atau kedua dari dua kuantitas yang tidak diketahui (untuk itu membutuhkan dua jumlah yang tidak diketahui untuk mengekspresikan hubungan antara dua titik) kurva milik kelas kedua; dan jika persamaan tersebut mengandung istilah tingkat kelima atau keenam dalam salah satu atau kedua kuantitas yang tidak diketahui, kurva tersebut termasuk kelas ketiga, dan seterusnya tanpa batas waktu (G, 48).

Poin yang sama dibuat kemudian dalam Buku Dua, di mana Descartes menekankan "tidak peduli bagaimana menyusun kurva untuk dijelaskan, asalkan itu salah satu yang saya sebut geometris," akan selalu mungkin untuk menemukan persamaan yang menentukan semua poin kurva (G, 56). Dia menegaskan kurva geometris dapat diklasifikasikan sesuai dengan persamaan mereka, tetapi juga menunjukkan dalam kelas tertentu, kesederhanaan kurva harus diberi peringkat sesuai dengan gerakan yang diperlukan untuk konstruksi. Misalnya, meskipun lingkaran milik kelas yang sama dengan elips, hiperbola, dan parabola, kurva terakhir ini adalah "sama-sama kompleks" sedangkan lingkaran "jelas merupakan kurva yang lebih sederhana" dan dengan demikian akan lebih berguna dalam pembangunan masalah ( G, 56).

Seperti dalam Buku Satu, Descartes menggunakan Masalah Pappus untuk menggambarkan kekuatan kalkulus geometrisnya, di mana dalam Buku Dua, tujuannya adalah untuk menunjukkan bagaimana klasifikasi aljabar kurva-nya membuatnya mudah "untuk menunjukkan solusi yang [dia] telah berikan masalah Pappus "(G, 59). Tujuan khusus di sini adalah untuk menetapkan kurva yang memecahkan Masalah Pappus umum adalah kurva geometris yang sah, yaitu, untuk menunjukkan kurva Pappus memenuhi standar konstruksi geometri yang tepat dan ketat yang baru saja ia susun. Diskusi Descartes tentang Masalah Pappus dalam Buku Dua dimulai sebagai berikut:

Setelah sekarang membuat klasifikasi umum kurva, mudah bagi saya untuk menunjukkan solusi yang telah saya berikan tentang masalah Pappus. Karena, pertama, saya telah menunjukkan [dalam Buku Satu] ketika hanya ada tiga atau empat baris persamaan yang berfungsi untuk menentukan poin yang diperlukan adalah dari tingkat kedua.

Oleh karena itu kurva yang mengandung titik-titik ini [yaitu, kurva Pappus] harus menjadi milik kelas pertama, karena persamaan tersebut menyatakan hubungan antara semua titik kurva Kelas I dan semua titik garis lurus tetap. Ketika tidak ada lebih dari delapan garis yang diberikan persamaan paling banyak merupakan biquadratic, dan oleh karena itu kurva [Pappus] yang dihasilkan milik Kelas II atau Kelas I. Ketika tidak ada lebih dari dua belas garis yang diberikan, persamaannya adalah derajat keenam atau lebih rendah, dan oleh karena itu kurva yang diperlukan milik Kelas III atau kelas bawah, dan seterusnya untuk kasus lain (G, 59).

Seperti ditunjukkan dalam bagian di atas, Descartes menetapkan dalam Buku Dua kurva Pappus jatuh ke dalam kelas-kelas kurva geometrik yang telah ditentukan, di mana kelas di mana kurva Pappus jatuh tergantung pada jumlah garis yang diberikan dalam masalah dan dengan demikian, pada tingkat persamaan di mana masalah berkurang.

Misalnya, ketika Descartes memperlakukan Pappus Problem empat-baris dalam Buku Dua, ia menunjukkan, dengan memvariasikan koefisien dari persamaan derajat kedua yang masalahnya telah dikurangi (melalui analisis Buku Satu), dapat membangun salah satu dari lingkaran, parabola, hiperbola, atau elips (G, 59-80). Artinya, dia menunjukkan kurva Pappus yang memecahkan masalah empat-baris adalah lingkaran atau salah satu dari bagian kerucut, kurva yang sangat "geometris" yang telah dia kelompokkan ke dalam Kelas I.

Dalam dua tahap, kemudian, Descartes telah menunjukkan solusi untuk Masalah Pappus umum. Dalam Buku Satu ia menawarkan analisis aljabar tentang masalah tersebut, dan dalam Buku Dua ia mengklaim untuk memberikan sintesis (atau demonstrasi) kurva yang memecahkan masalah umum adalah kurva geometri yang sah yang memenuhi standar yang dinyatakannya untuk ketepatan dan presisi geometris.

Dan dengan dua tahap ini selesai, Descartes mengklaim ke Mersenne enam bulan setelah La Geometrie diterbitkan perlakuannya terhadap Masalah Pappus umum adalah bukti metode barunya untuk pemecahan masalah geometris adalah peningkatan dari metode pendahulunya:

Saya tidak suka harus berbicara baik tentang diri saya sendiri, tetapi karena ada beberapa orang yang dapat memahami Geometri saya, dan karena Anda ingin saya memberi tahu Anda apa pandangan saya sendiri tentang itu, saya pikir sudah sepantasnya saya harus memberi tahu Anda itu sedemikian rupa sehingga saya tidak dapat berharap untuk memperbaikinya.

Dalam Optik dan Meteorologi saya hanya mencoba menunjukkan metode saya lebih baik daripada yang biasa; dalam Geometri saya, bagaimanapun, saya mengklaim telah menunjukkan ini. Tepat di awal saya memecahkan masalah yang menurut kesaksian Pappus tidak satupun dari orang dahulu berhasil memecahkan; dan dapat dikatakan tidak ada orang modern yang dapat menyelesaikannya juga, karena tidak ada dari mereka yang menulis tentang itu, meskipun yang paling pintar dari mereka telah mencoba untuk menyelesaikan masalah lain yang disebutkan Pappus di tempat yang sama dengan yang telah ditangani oleh orang dahulu.

Sebesar kepercayaan Descartes dalam pemecahannya untuk Masalah Pappus, ada pertanyaan yang melingkupi sintesisnya tentang masalah umum dalam Buku Dua.

Seperti ditunjukkan di atas, Descartes berupaya menetapkan melalui sintesisnya kurva yang menyelesaikan Masalah Pappus adalah "geometris" menurut standarnya sendiri, yaitu, kurva Pappus dapat dikonstruksi oleh gerakan "tepat dan tepat" yang diperlukan untuk membangun dengan benar kurva geometris. Namun, sama sekali tidak jelas Descartes telah membuktikan hal ini. Bahkan ketika membahas Masalah Pappus empat baris dasar dalam Buku Dua, Descartes tidak menarik bagi gerakan yang jelas dan berbeda saat ia membangun kurva Pappus yang memecahkan masalah (dalam hal ini, lingkaran, parabola, hiperbola, dan elips).

Sebaliknya, ia bergantung pada teori kerucut Apollonius, yang mengharuskan kerucut dipotong pada titik yang ditentukan di dalam pesawat, dan seperti yang dikatakan Bos, teknik Apollonia untuk membangun kerucut ini "bukanlah metode konstruksi yang segera menghadirkan dirinya ke pikiran. sebagai jelas dan berbeda ". Khususnya, karena tidak jelas bagi matematikawan pada saat itu apakah konstruksi yang membutuhkan penempatan kerucut di pesawat memenuhi standar yang tepat dan ketat dari penalaran geometris, perlakuan Descartes pada kurva Pappus dalam kasus empat baris ini tidak meyakinkan menunjukkan mereka. Status "geometrik". Kemudian di Buku Dua, ketika dia menangani Masalah Pappus lima baris, masalahnya menjadi lebih rumit.

Ingatlah selain penekanannya pada gerakan "tepat dan tepat" yang dapat digunakan untuk menggambarkan kurva geometris yang sah, Descartes juga mengklaim kurva ini "dapat dipahami sebagai digambarkan oleh gerakan terus menerus atau dengan beberapa gerakan berturut-turut." seperti itu, cukup berharap konstruksi geometris dari kurva-kurva ini tidak boleh berjalan dengan cara yang sama seperti Buku Satu, di mana Descartes membangun kurva Pappus dengan menyelesaikan persamaan yang menjadi masalah pengurangan masalah tersebut. Namun, ketika Descartes memperlakukan Masalah Pappus lima baris dalam Buku Dua, ia sebenarnya menawarkan konstruksi titik-titik dari kurva Pappus. Dia kemudian menyatakan konstruksi searah dari kurva Pappus "geometris" ini sangat berbeda dari konstruksi searah kurva non-geometris, "mekanis":

Perlu dicatat ada perbedaan besar antara metode ini di mana kurva [Pappus] dilacak dengan menemukan beberapa titik di atasnya, dan yang digunakan untuk kurva spiral dan yang serupa. Dalam yang terakhir, tidak ada titik kurva yang diperlukan dapat ditemukan dengan senang hati, tetapi hanya titik-titik seperti yang dapat ditentukan oleh proses yang lebih sederhana daripada yang diperlukan untuk komposisi kurva ... Di sisi lain, tidak ada titik pada ini ["Geometris"] kurva yang memasok solusi untuk masalah yang diusulkan yang tidak dapat ditentukan oleh metode yang saya berikan (G, 88-91).

Saran dari Descartes adalah ketika secara searah membangun kurva geometris, dapat mengidentifikasi titik yang mungkin pada kurva, dan segera setelah pernyataan di atas, melanjutkan untuk menyamakan kurva yang dibangun dengan cara ini dengan kurva yang mungkin dapat dibangun dengan gerakan kontinu. : "Metode penelusuran kurva ini dengan menentukan sejumlah titik yang diambil secara acak hanya berlaku untuk kurva yang dapat dihasilkan oleh gerakan reguler dan kontinu" (G, 91).

Perbedaan antara konstruksi kurva "geometris" dan "mekanis" ini memiliki dua tujuan yang agak penting dalam program La Geometrie : (1) Descartes dapat menetapkan kurva Pappus yang telah ia buat secara pointwise sebenarnya adalah "geometris" dan dengan demikian lengkap sintesis (atau demonstrasi) dari Masalah Pappus umum, dan (2) ia dapat mempertahankan batas antara kurva "geometris" yang dapat dipahami dan kurva "mekanis" yang tidak dapat dipahami.

Tanpa indikasi yang jelas mengapa konstruksi kurva Pappus yang menunjuk ke titik adalah "geometris," Descartes harus membiarkan kurva "mekanis" seperti spiral dan quadratrix ke dalam domain kurva geometris, karena kurva ini juga dapat dibangun dengan cara yang tajam. Ingatlah misalnya konstruksi quadratrix yang menunjuk Clavius.

Menurut deskripsi Clavius, mulai dengan kuadran lingkaran dan kemudian mengidentifikasi titik-titik persimpangan antara segmen yang membagi dua kuadran dan segmen yang membagi dua busur kuadran. Yaitu, kami mengidentifikasi beberapa titik berpotongan segmen yang dapat dibangun dengan penggaris lurus dan kompas, dan kemudian, untuk menghasilkan quadratrix, kami menghubungkan titik-titik perpotongan, yang ditempatkan secara merata di sepanjang kurva yang dicari.

Mengapa konstruksi seperti itu tidak "geometris"? Karena, menurut Descartes, jika melanjutkan seperti Clavius, "tidak ada titik kurva yang diperlukan dapat ditemukan dengan senang hati." Secara khusus, mengingat pembatasan konstruksi Euclidean, hanya dapat membagi busur yang diberikan menjadi 2 bagian n . Dengan demikian, apa yang disarankan oleh Descartes adalah tidak mungkin untuk membagi busur dengan cara apa pun yang inginkan, dan oleh karena itu tidak dapat menemukan titik sembarang di sepanjang kurva dengan menggunakan konstruksi pointwise.

Namun dalam kasus kurva "geometrik", dapat menemukan titik sembarang pada kurva dengan mengajukan banding ke persamaan yang sesuai dengan masalah; atau meminjam terminologi Bos, Descartes mengklaim kurva "geometris", dan kurva Pappus pada khususnya, dapat dihasilkan oleh konstruksi "umum" yang mengarah ke titik.

(dok. pribadi)

Sementara pertimbangan konstruksi Clavius dari quadratrix menawarkan beberapa alasan untuk menerima perbedaan Descartes antara berbagai jenis konstruksi yang searah, masih ada klaim kontroversial kurva yang digambarkan oleh "generik" konstruksi searah adalah kurva yang dapat dibangun dengan gerakan kontinu. Identifikasi ini memungkinkan Descartes untuk menetapkan kurva Pappus sebagai kurva "geometris", tetapi ia tidak menawarkan bukti identitas, dan dengan demikian, ada pertanyaan apakah Descartes sebenarnya menunjukkan kurva Pappus "geometris" menurut standarnya sendiri. 

Ada pertanyaan lebih lanjut seputar kriteria Descartes untuk kurva "geometris". Seperti yang telah di lihat di atas, perhatian eksplisit Descartes dalam Buku Dua adalah untuk menawarkan standar untuk kurva geometris yang terikat dengan gerakan yang jelas, jelas dan berbeda yang diperlukan untuk konstruksi mereka.

Namun, baru-baru ini menawarkan kasus yang meyakinkan di balik pernyataan eksplisit Descartes di La Geometrie terdapat masalah yang lebih mendasar: Untuk memastikan kurva tersebut, para ahli matematika telah menggunakan untuk menyamakan lingkaran, seperti spiral dan quadratrix yang secara eksplisit disebutkan.

Dalam Buku Dua, diterjemahkan non-geometris. Mancosu mendukung kasusnya dengan bukti dari korespondensi Descartes yang menunjukkan, bagi Descartes, dalam beberapa kasus memang mungkin untuk memahami secara jelas dan jelas hubungan antara garis lurus dan lingkaran, suatu hubungan yang dia anggap tidak tepat di La Geometrie . Yaitu, dalam surat 1638 untuk Mersenne, Descartes menulis,

Anda bertanya kepada saya apakah saya pikir bola yang berputar di pesawat menggambarkan garis yang sama dengan kelilingnya, yang saya balas ya, menurut salah satu prinsip yang saya tulis, yaitu apa pun yang bayangkan dengan jelas dan jelas adalah benar. Karena saya memahami dengan baik garis yang sama kadang-kadang bisa lurus dan kadang-kadang melengkung, seperti string.

Di La Geometrie, hubungan antara garis lurus dan kurva dianggap tidak tepat karena, sebagaimana Descartes katakan, "rasio antara garis lurus dan kurva tidak diketahui, dan saya percaya tidak dapat ditemukan oleh pikiran manusia" (G, 91). Descartes yang kemudian mengakui dengan jelas dan jelas memahami hubungan seperti itu menunjukkan, menurut Mancosu, kriteria yang dinyatakan untuk kurva geometris yang disajikan dalam La Geometrie hanya mengungkapkan sebagian dari agenda matematika Descartes. Potret yang lebih lengkap harus, Mancosu berpendapat, memperhitungkan komitmen Descartes terhadap ketidakmungkinan mengkuadratkan lingkaran.

Apakah Descartes memiliki agenda tersembunyi yang disarankan Mancosu, klaim eksplisit yang digunakan untuk mendefinisikan program pemecahan masalah yang disajikan dalam La Geometrie menunjukkan keterbatasan matematika Descartes. Seperti yang telah lihat di atas, fokus utama Descartes adalah pada standar untuk "ketepatan penalaran" geometri yang terikat pada gerakan yang jelas dan berbeda untuk konstruksi dan pada persamaan hingga untuk merepresentasikan kurva yang dibangun sedemikian.

Akibatnya, tidak ada ruang dalam program La Geometrie untuk menggunakan tak terhingga dalam konstruksi kurva atau untuk merawat kurva yang diwakili oleh persamaan tak terbatas. Karena itu, Descartes menghilangkan dari program geometrisnya unsur-unsur penalaran matematis dan geometris yang memungkinkan bagi Newton dan Leibniz untuk mengembangkan kalkulus pada akhir abad ketujuh belas.

Meskipun demikian, mengingat betapa cepatnya Descartes mengasah keterampilan matematika dan seberapa cepat ia mengembangkan program inovatif untuk geometri, tidak akan terlalu berisiko untuk menerima penilaian diri Descartes dan mempertahankan keyakinan kalkulus akan berada dalam jangkauannya seandainya ia mempertimbangkan infinitesimal dan infinite:

Setelah menentukan seperti yang saya lakukan [di La Geometrie ] semua yang dapat dicapai dalam setiap jenis masalah dan menunjukkan cara untuk melakukannya, saya mengklaim orang-orang seharusnya tidak hanya percaya saya telah mencapai lebih dari para pendahulu saya tetapi juga harus diyakinkan anak cucu tidak akan pernah menemukan apa pun dalam subjek ini yang tidak mungkin saya temukan dengan baik jika saya repot-repot mencarinya.

Daftar Pustaka:

Bos, Henk J.M., 1981, "On the representation of curves in Descartes' Gomtrie," Archive for History of Exact Sciences 24: 295--338.

__, 2001, Redefining Geometrical Exactness: Descartes' Transformation of the Early Modern Concept of Construction. New York, Berlin, Heidelberg: Springer-Verlag.

Descartes, Rene, 1637, The Geometry of Rene Descartes with a facsimilie of the first edition, translated by David E. Smith and Marcia L. Latham. New York: Dover Publications, Inc., 1954. [cited as G followed by page number]