Penghitungan Value at Risk Menggunakan Distribusi Generalized Extreme Value

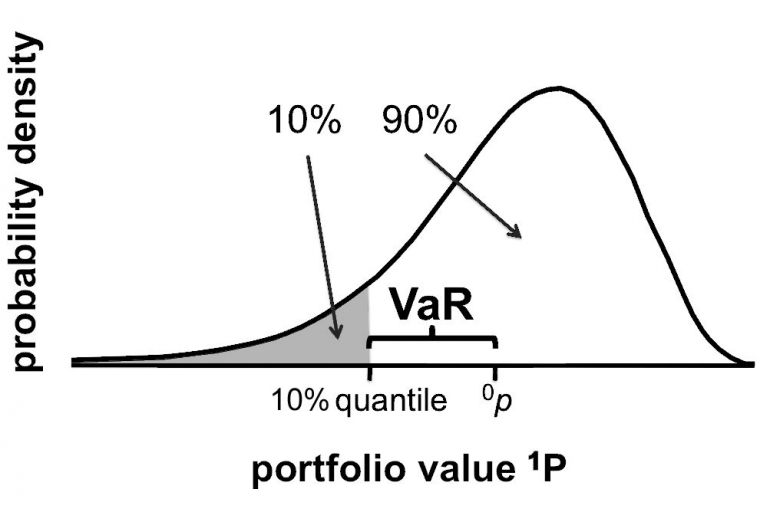
Di dalam investasi, Value at Risk (VAR) merupakan salah satu cara untuk mengukur besarnya risiko atau potensi kerugian yang mungkin terjadi pada portofolio yang dimiliki investor. Bank sangat memerlukan pengukuran risiko market risk dengan menggunakan metode Value at Risk ini agar dapat mengalokasikan biaya dan memperkuat modal untuk mempersiapkan diri terhadap akibat kerugian yang mungkin timbul.  Potensi kerugian ini didefinisikan untuk suatu jangka waktu tertentu (time horizon) dan nilai probabilitas tertentu (confidence level).

Misal portofolio yang bernilai Rp 100.000.000,- dan memiliki VaR bulanan sebesar Rp 9.500.000,- dengan tingkat kepercayaan 99%. VaR disini artinya bahwa ada kemungkinan 1% kerugian lebih dari Rp 9.500.000,- dalam holding period yang didefinisikan dalam kondisi pasar normal. 

Baca juga: Simulasi Monte Carlo dengan Excel

Dalam menghitung VaR terdapat beberapa asumsi yang perlu diperhatikan, salah satunya adalah distribusi data. Setiap distribusi memiliki cara perhitungan VaR yang berbeda. Salah satu distribusi yang dapat mencerminkan data closing price saham bulanan adalah distribusi Generalized Extreme Value karena pada closing price terdapat beberapa price yang memiliki risiko low frequency high severity. Nilai ekstrem berasal dari suatu peristiwa yang sangat jarang terjadi sehingga sering disebut dengan catastrophic losses.

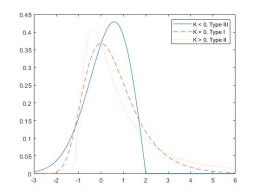
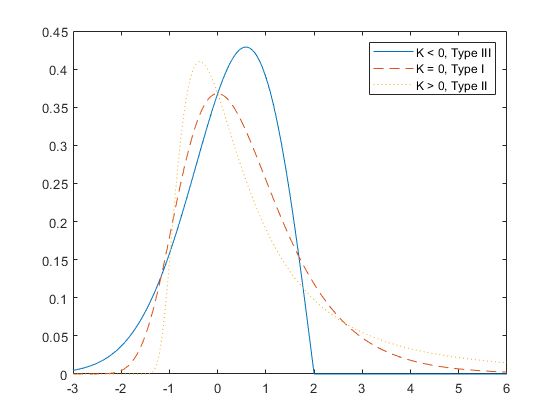
Distribusi Generalized Extreme Value memiliki 3 parameter yaitu parameter shape, scale, dan location. Berdasarkan nilai parameter shape, distribusi Generalized Extreme Value dapat dibedakan dalam tiga tipe yaitu :

1. Tipe I (Distribusi Gumbel), jika nilai shape = 0
2. Tipe II (Distribusi Frechet), jika nilai shape > 0
3. dan Tipe III (Distribusi Weibull), jika nilai shape < 0

Sumber gambar : www.mathworks.com

Semakin besar nilai shape, maka distribusinya akan memiliki ekor yang semakin berat (heavy tailed). Dengan demikian, dari ketiga tipe distribusi di atas, yang memiliki ekor paling berat adalah Distribusi Frechet. 

Nilai VaR yang diperoleh harus diuji validasi terlebih dahulu, salah satunya dengan menggunakan metode back testing. Back testing adalah suatu metode yang digunakan untuk menguji validitas model VaR yang dibangun berdasarkan realitas pasar sehingga dapat dilihat seberapa besar model VaR tersebut menggambarkan data aktual historis pasar.

Baca juga: Pembahasan Soal untuk Lebih Memahami Aktiva/Asset Lancar

Data yang digunakan dalam penelitian ini adalah data sekunder harga penutupan (closing price) saham bulanan pada PT. Astra Internasional Tbk. (ASII.JK) periode Juni 2015 sampai dengan Juni 2019 dengan jumlah data sebanyak 60. Data penutupan harga saham tersebut dapat diakses melalui situs investing.com.  Software statistik yang digunakan pada penelitian ini adalah R Studio (R version 3.5.1).

Sumber gambar : www.mathworks.com

Berikut langkah-langkah yang dilakukan: 

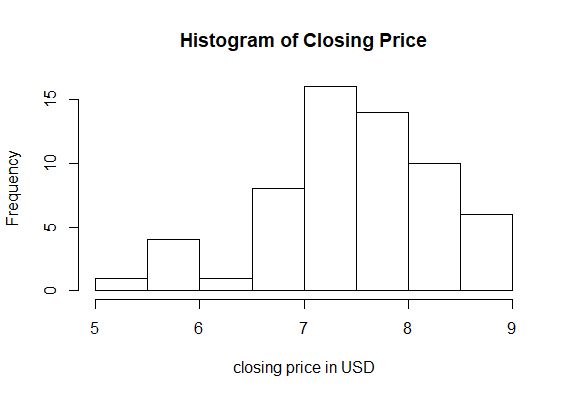
1. Mengumpulkan data bulanan closing price dari tahun 2015-2019
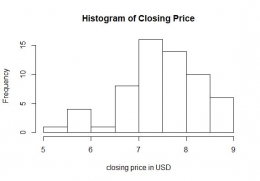
2. Fitting data untuk melihat distribusi dari data. Dari output visual dengan histogram dapat dilihat bahwa data berdistribusi Generalized Extreme Value. Untuk meyakinkan bahwa data berdistribusi Generalized Extreme Value digunakan pula goodness of fit test Anderson Darling,
   dengan 0 adalah data berdistribusi Generalized Extreme Value. Diperoleh p-value sebesar 0.474, dengan menggunakan sebesar 5% maka 0 tidak ditolak sehingga dapat disimpulkan bahwa data berdistribusi Generalized Extreme Value.
3. Menghitung parameter untuk distribusi Generalized Extreme Value. Diperoleh shape = -0.4698087, scale = 0.8662159, dan location = 7.2916394. Dikarenakan nilai < 0 maka data closing price saham bulanan berdistribusi Generalized Extreme Value tipe III (Distribusi Weibull).
4. Hitung nilai VaR menggunakan rumus   = - (location/scale) [1 - (- log )^-shape]. Digunakan confidence interval 90% dan 95% untuk perbandingan. Dengan menggunakan confidence interval 90% diperoleh nilai VaR sebesar USD8.494856 sedangkan untuk confidence interval 95% diperoleh nilai VaR sebesar USD8.67865.
5. Selanjutnya langkah terakhir adalah validasi apakah model VaR baik digunakan. Menggunakan uji kupiec dengan 0 adalah
   ( x > nilai VaR) p* (model VaR baik digunakan) dimana p* adalah 1- confidence interval. Untuk VaR dengan confidence interval 95% diperoleh nilai p-value 1 dan untuk confidence interval 90% diperoleh nilai p-value 0.674187, dengan nilai =5% maka 0 tidak ditolak. Sehingga dapat disimpulkan bahwa model VaR baik digunakan untuk confidence interval 90% maupun 95%.

Baca juga: Penjelasan yang Mudah Mengenai Cost of Capital (Biaya Modal)